0. 前言

之前在 Luna Tech | 聊聊计算机的几个基本概念 一文中，我提到了数据结构这个概念，数据结构用一句话解释就是：整理、管理数据的方式。

今天我们就来具体聊聊数据结构（Data Structure）。

1. 数据结构基本概念

数据结构是啥？

数据结构是排列组合数据的方式。

为什么需要数据结构？

很简单，数据多了，咱就有整理的需求啊。

数据都分门别类整理好了，要用的时候找起来就方便多了嘛（想象一下你的衣柜）。

更重要的是，有了数据结构，我们就可以更快更好地满足 4 大常见需求。

4 大需求

通常来说，我们对数据（衣服）有 4 大常见需求：增查改删。

增（Add）：加一个新数据（买一件新衣服）；

查（Search）：找一个已有数据（找一件想穿的衣服）；

改（Modify）：改变数据（把长裤剪成 7 分裤）；

删（Delete）：删除数据（这衣服太旧了，扔了！）

回忆一下数据类型（Data Type）的知识

Composite 类型需要通过数据结构来排列组合 Primitive 类型和 Composite 类型的数据。

Abstract 类型只是定义了数据的预期行为，具体还是要通过某种数据结构实现【美好构想】。

数据结构和数据类型有千丝万缕的关系~

2. 数据结构分类

有些教程里面会说数据结构分为 primitve 和 non-primitive，non-primitive 再分为线性和非线性，但我认为这样的分类混淆了数据类型和数据结构的概念（Primitive 是一种数据类型，不是数据结构）。

所以我认同的数据结构分类是：线性（Linear）和非线性（Non-Linear），不考虑 Primitive Data Type。

线性和非线性的区别

Difference between linear and non-linear data structure

线性数据结构是根据【某种顺序】来把数据排成【一个队列】（好比做广播体操的时候，所有人排成一竖排）；

非线性数据结构呢？这种数据结构并不是简单地把数据排成一个竖排，数据可以根据不同的方式和内在关系来排列组织，可以有多个维度，这种数据结构也显然更加复杂。

线性数据结构

包含 Array（数组）、List（列表）。

非线性数据结构

可以细分为：Tree（树）、Hash Table（散列表/哈希表）、Graph（图）。

3. 线性数据结构

1. Array（数组）

Array 是一个容量有限的，可以包含多个数据的线性数据结构；我们通过数据的位置编号（index）来进行【增查改删】。

1
2
3
4
5

// 这是一个由 string 组成的 Array
string[] colors = {"Red", "Green", "Yellow", "White", "Blue", "Black"};

// 通过 index 来找到数据（从 0 开始）
string red = colors[0];

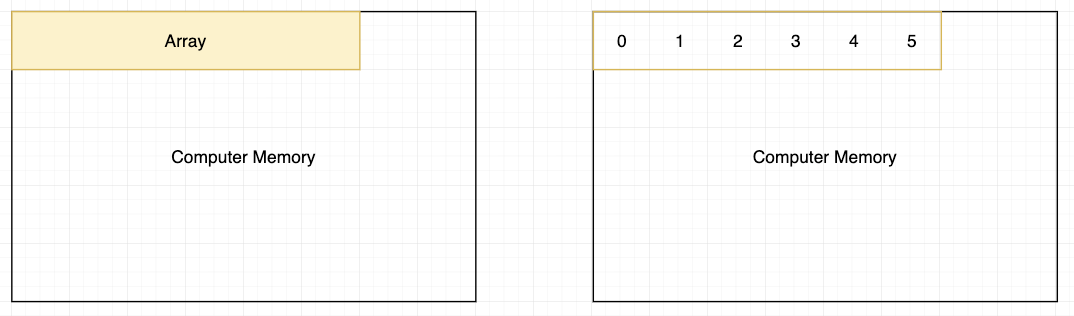
Array 本质上就是在计算机存储空间里面的一个连续块。

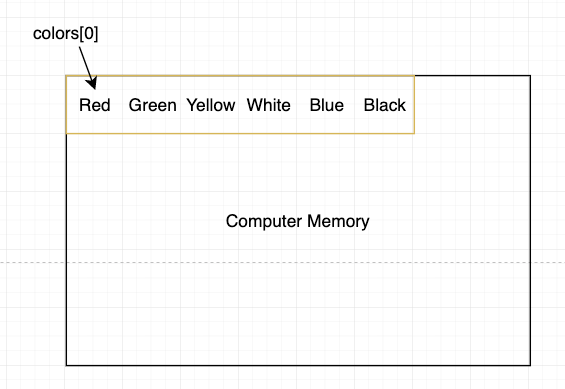
当我们创建 colors 这个 array 的时候，这个 array 的指针会指向第一个值，也就是 Red。

由于 Array 的本质是一个连续的储存空间，在创建 Array 的时候，我们必须告诉计算机，这个储存空间的大小到底是多少（10？100？1000？）。

而且呢，在很多语言中，Array 创建之后，储存空间的大小就不能改啦（immutable type）。

也有一些支持 dynamic array 的语言，支持更改 Array 的储存空间；比如 C++ 里面的 vector，Java 里面的 ArrayList，在此不做具体展开。

2. Linked List（链表）

Linked List 是 List 这种 Abstract Data Type 的实现方式。

这种数据结构和 Array 的最大区别在于，不需要占用一块连续的 memory 空间，可以零散地分布。

链表中的每一个成员，都是一个 node。

每个 node 包含两部分：

1. 数据（data）
2. 指针（pointer）

指针是用来干嘛的？

用来指向下一个 node 的内存地址。

如何找到链表中的某个 node？

之前我们讲过，Array 是根据 element 的 index 来寻找的，由于链表并没有用到一块完整的 memory，我们没法用 index 来找寻 node 了 o(╥﹏╥)o

唯一的方法就是根据数据查询，我们需要从第一个 node 开始，逐个 node 查询，直到找到我们想要的数据为止。

万一数据重复了咋办？

链表是允许有重复数据的，所以你只有遍历全部的 node 才能确定某个数据到底是否有重复。

假如你要增加一个 node 怎么办？

如果这个新的 node 是放在 list 最前面，很简单，我们只需要把新的 node 里面的 pointer 指向之前的第一个 node。

假如我们要把新的 node 放在最后（或者中间）呢？

我们只能从第一个 node 开始，一个个的找，直到找到最后（中间）的 node，然后再把新的 node 加上去（是不是效率低了很多呀~）。

3. Doubly Linked List （双向链表）

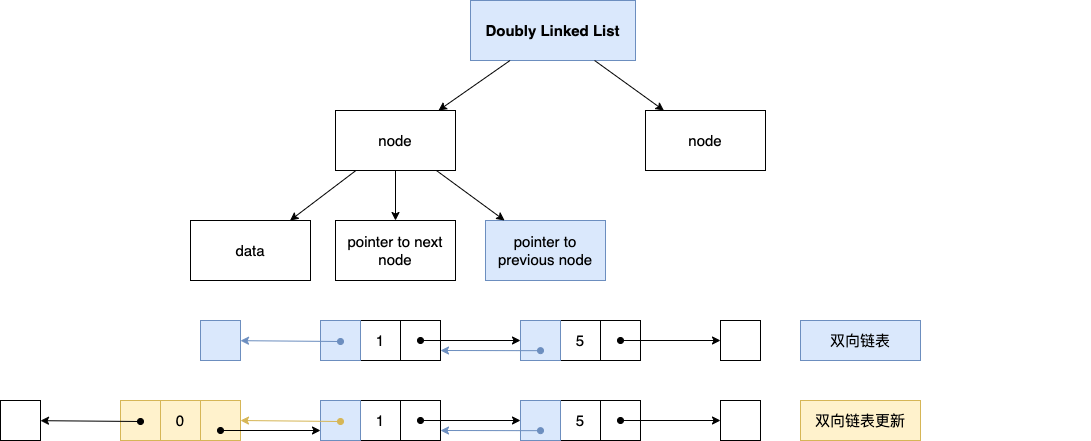
这种数据结构和 Linked List 唯一的区别就是：node 里面除了有 data, 指向下一个 node 的指针，还多了个【指向前一个 node】的指针（所以叫双向嘛）。

这种数据结构听起来很棒，但是也有个缺点，那就是每当 List 里面 node 的位置发生变化时，我们需要 update 两个 pointer（单向链表只需要 update 一个）。

4. 非线性数据结构

1. Tree（树）

树结构指的是像树一样的有层次感的结构（感觉说了句废话）。

Tree 是一种 Abstract Data Type (ADT)。

大家观察一下这颗树，是不是有树根（root），是不是有树枝（branch），是不是有树叶（leaf）？

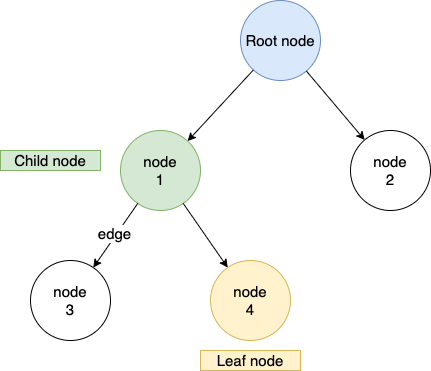
树结构的灵感就来源于大自然，我们有一个 root node（树根），从 root node 里面可以生长出多个 child node。

每个 node 都有 data，因为 node 是长出来的，所以每个 node 也有树枝相连接（称为 edge）。

Edge 就代表了 node 与 node 之间的关系，我们可以根据 edge 找到每个 node 的家长。

那树叶呢？

因为树叶上不能再长树枝，所以没有 child 的 node 就被称为 leaf node。

各种各样的树结构（以后再讲）

1. General Tree
2. Binary Tree
3. Binary Search Tree
4. Red-Black Tree
5. B-tree
6. ……

2. Hash Table（哈希表）

这种数据结构的最大特点就是：Key-Value pair（键值对）。

什么意思呢？就好比你手头有一本字典，想要查到一个单词，必须在目录里面找到页码。

字典的目录就是 Hash Table，Hash Table 里面存的是 Hash Value，Hash Value 是通过 Hash Function 和 Key 生成的。

通过 Hash Value 可以找到 Key-Value pair。

Hash Value 就好比单词的页码，有了 Hash Value 你就能找到 Key-Value pair（单词）。

这种 Hash Value 和 Key-Value pair 一一对应的关系也被称作 Associative Array（关联数组）。

Associative Array 是一种 ADT，特征是 Key-Value Pair，在 Array 里面每个 key 都是独一无二的。 Associative Array 也可以称作 Map（映射）、Dictionary（字典），它们都是一个东西。

1
2
3

Dictionary<string, string> dict = new Dictionary<string, string>();
dict.Add("key1", "value1");
dict.Add("key2", "value2");

需要注意的是：key 必须是独一无二的。

Hash Table 是如何创建的呢？

Introduction to Hashing and its uses

哈希碰撞和生日攻击

Hash Function（散列函数）是 Hash Table 的幕后推手。

每个 Key-Value pair 里面的 key，都会通过一个 hash function（哈希函数）来创建一个 hash value（哈希值），hash value 就存在 hash table 里面。

Hash Table 的作用是让计算机更快地找到 key value pair。

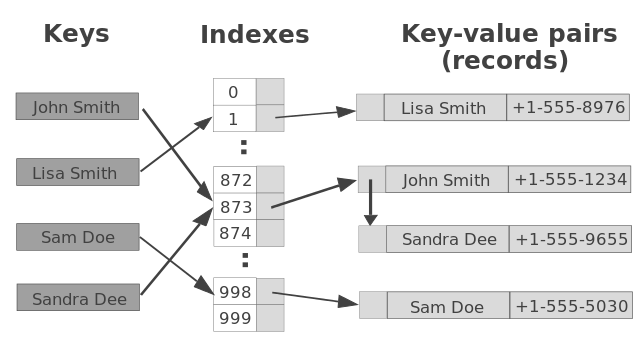
比如下图，我们可以看到，不同的 key 对应了不同的 hash value。

假如不同的 key 通过 hash function 生成了一样的 hash value，就说明发生了冲突（Collision）。

我们之前讲过每个 bit 有 0 和 1 两种可能性，如果 hash value 是 10 bit，那么总共的可能性 = 2^10 = 1024。

也就是说，10 bit 的 hash value 只能满足 1024 个 unique key，再多了肯定会冲突。

hash value 的 bit 越多，发生冲突的可能性越小，但是每个值所占用的储存空间也越大。

所以我们需要在储存空间和发生冲突之间寻找平衡，针对不同的需求设计不同的 hash function。

hash function 越好，生成的 hash value 越无序。

比如 “a” 生成的 hash value = 1, “b” 生成的 hash value = 2，那大家很容易猜到 “c” 对应的 hash value，这就是一个比较失败的 hash function。

大部分时候，编程语言的 Hash Table 已经帮我们搞定 Hash Function 了，大家放心大胆地直接用这个数据结构就行啦~

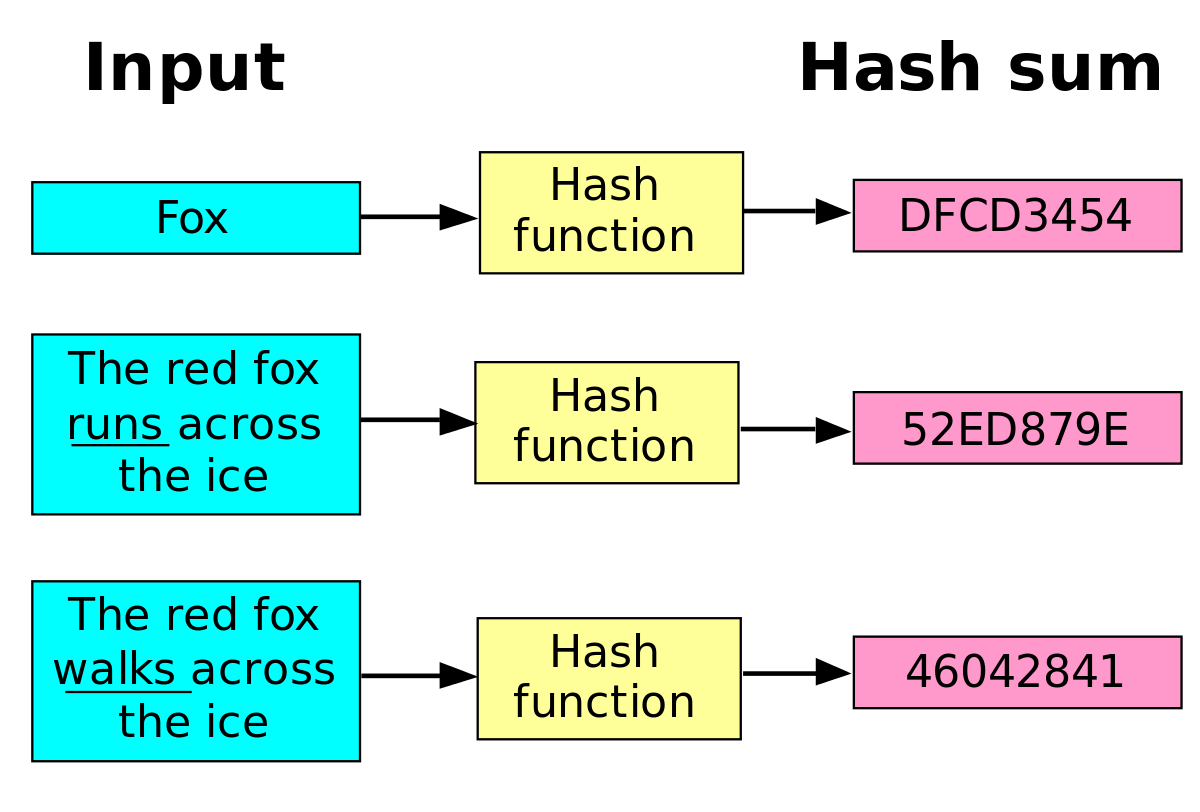
Hash Function 的应用

Hash Function 是密码学的一个重要分支，因为它可以把 input （输入的信息）转换为固定长度的 output（密码），而且是不可逆的（知道了 output 也无法逆向演算出 input）。

MD5（消息摘要算法）和 SHA（安全散列算法）是哈希函数的典型。

MD5 生成的 hash value 有 128 bit；SHA-2 生成的 hash value 有 256 bit。

另外，Hash 也常用于压缩，帮助我们节省空间，保存数据。

3. Graphs（图）

图也是一种 Abstract Data Type（ADT） ，这种数据类型是根据 graph theory（图论）的原则来设计的。

Graph 数据结构包含两个部分：

1. nodes：图上的一个个点
2. edges：用来连接点的线

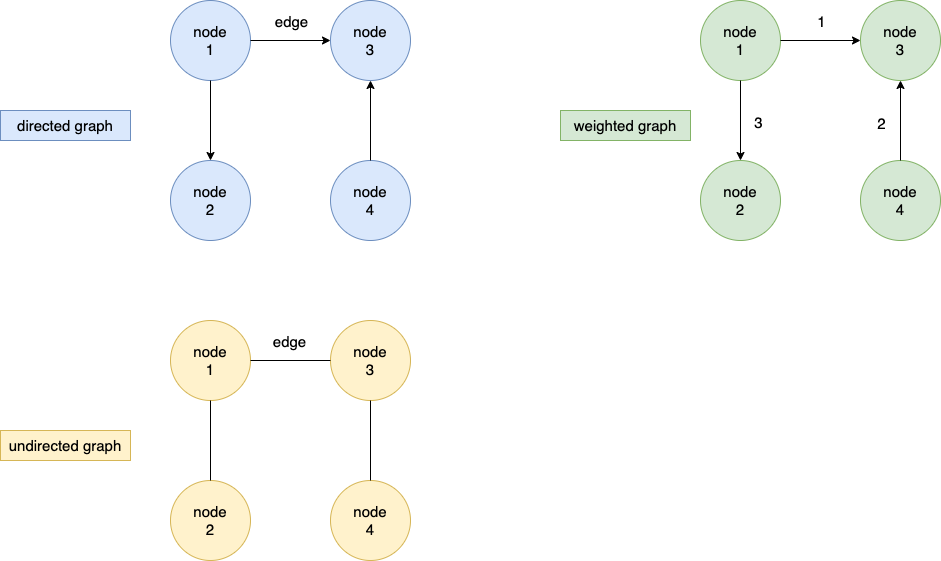
图分为两种：

1. 有方向的图（directed graph）
2. 没方向的图（undirected graph）

方向就是 edge 的箭头，如果 edge 带箭头，就说明有方向（是不是很好理解呀）。

Weighted Graph（加权图）

这种图的特点是，每个 edge 都有一个数字用来表明重要程度。

图的用途

图可以用来表明关系，比如你和你的微信好友之间的关系；如果你们经常聊天，可以用加权图来表示你和不同好友之间的关系密切程度。

5. 图结构和树结构的区别

大家看到这里可能会想，图和树看起来有点像啊~ 它俩到底有什么区别呢？

一句话：树是图的一种形式。

图包含树，树属于图。

1 - 方向

树是有方向的，每一颗树，都从 root 开始，分出不同的 branch 和 leaf；

但是图可以是没有方向的，而且任意一个 node 都可以作为起点，没有特定的 root node。

2 - 家长

树结构里面，每一个 node 只有一个家长，不能有爸爸+妈妈；

但图就无所谓了，每个 node 都可以有多个家长。

3 - path

在树结构里面，每两个 node 之间只有一条 path；

但是图结构里面，每两个 node 之间可以有多条 path。

图和树的区别

6. 结语

本文主要内容：

1. 数据结构分为线性和非线性两种
2. 线性包含 Array 和 List
3. 非线性包含 Tree, Hash Table, Graph
4. Array 和 List 的最大区别在于是否使用连续的内存
5. Tree 是一种特殊的 Graph
6. Hash Table 需要理解 Hash Function 和 Hash Value