Luna Tech | 聊聊树结构(Tree)

0. 前言
之前提到树结构是非线性数据结构的一种,也是图结构的一种特殊形式。
如果你经常听到二叉树、红黑树之类的名词,但是并不完全了解这些树的含义,那么就跟我一起学习一下吧~
树结构常见术语
- node(节点):这是树结构的基本元素,节点的名字 = key,节点包含的信息 = value 或 payload;
- edge(枝干):这也是一个基本元素,用来连接两个 node,表示它们之间的关系,每个 node (除root之外)都有一个来自其他 node 的 incoming edge,每个 node 可以有多个 outgoing edge;
- root(根节点):树结构里面唯一没有 incoming edge 的节点;
- path(路径):一个有序的节点集合,代表从 x 节点到 y 节点所经过的所有节点;
- children(子节点):incoming edge 为同一个 node 的所有 node;
- parent(父节点):一个有 outgoing edge 的节点;
- sibling(兄弟节点):共享一个 parent node 的所有 child node;
- subtree(子树):一个包含 node 和 edge 的分支;
- leaf node(叶节点):没有 child 的节点;
- level(层级):一个 node 的层级 = 这个 node 从 root 开始到自己所经过的 edge 的个数,root level = 0;
- height(高度):树的高度 = 树的最大层级;
树的定义
- Recursive:树要么是 empty,要么包含一个 root 和 >= 0 个 subtree,每个 subtree 都是一颗独立的树;每个 subtree 的 root 都通过一个 edge 跟 parent tree 的 root 进行连接;
- Binary:树包含 node 和 edge,有一个 root node,每个 node(除 root)都由 edge 和其他 node 进行连接,树的 root 可以经过 unique path 到达任何一个 node,每个 node 最多有两个 child,这种树就是二叉树。
1. Binary Tree(二叉树)
Binary Tree 是一种数据结构。
这种树的特点是,每一个 node 最多有两个 child node。
为什么是两个呢?因为每个 bit 有两种可能性,所以这棵树参考了 bit 的基本特征。
每个 node 和 root node 之间的距离是可以计算的。
二叉树是所有树的祖宗,也是最基本的树。
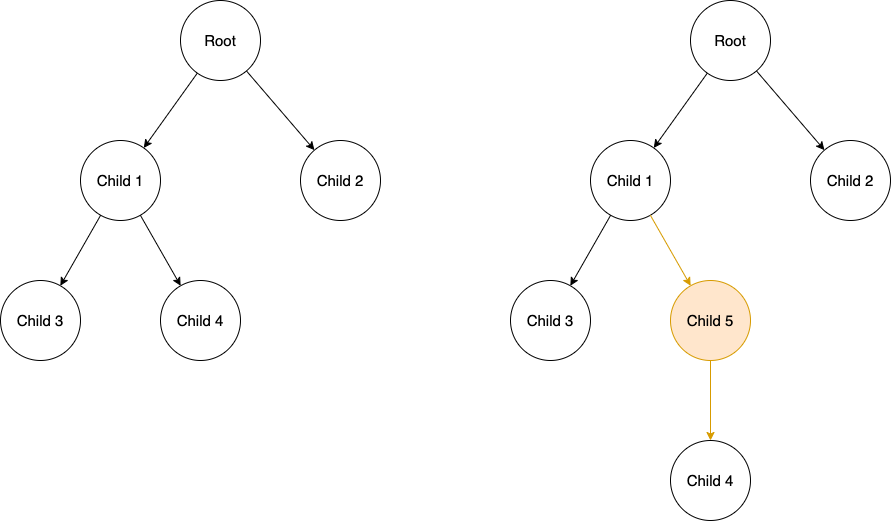
因为每个 node 上面最多只能有两个 child node,所以当我们【增查改删】的时候,需要考虑 node 之间的距离,以及让树重新找到平衡(假如一个 node 上有 3 个 child 就不平衡了嘛)。
找到平衡的意思就是把 edge(指针)指向的地址改一改。
比如我们在 child 4 的位置加了个 child 5,我们就必须修改一些指针,让它们正确的连起来。
2. Search Tree(查找树)
程序员的世界里还有另一种树,叫做查找树。
为啥叫查找树呢?
顾名思义,就是用来查东西的树,在这种树上,搜索特别方便,特别快捷。
查找树为什么方便查找呢?
因为所有的 node 都是经过排序的,有了排序自然就好找啦。
比如让你从 1 - 100 里面,找一个数字(30),如果这 100 个数字是无序的,那你运气不好的话要找 100 次才能找到。
假如这 100 个数字是排好顺序的,那你就可以用二分法,先找 50,再找 25……这样一来查找就特别有效率了对不对?
3. 各种各样的树
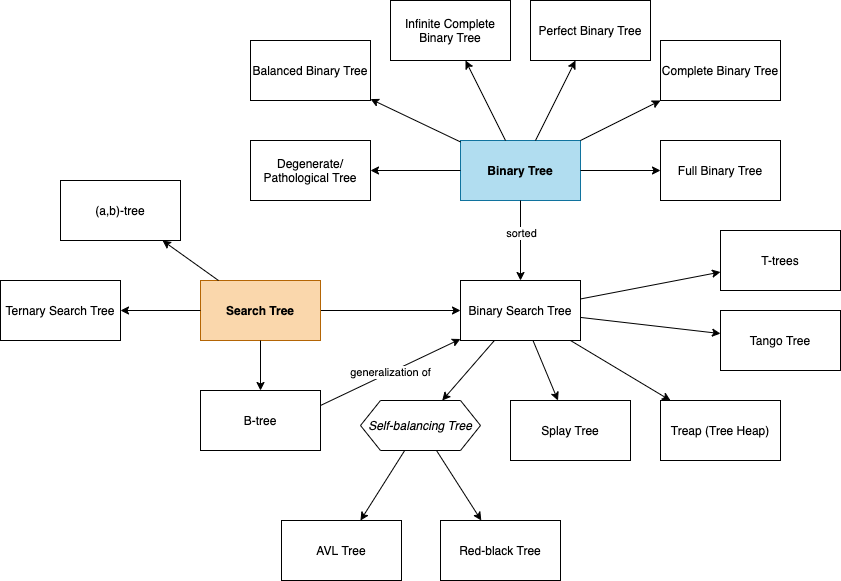
我经过查询之后,发现几乎所有的树都是由二叉树和查找树演变而来的,在这里奉上一张总结图。
4. Binary Search Tree(二叉查找树)
既然有二叉树和查找树这两个大类,那么我们不如创造一种方便查找的二叉树吧!
于是二叉查找树诞生了。
Binary Search Tree 简称 BST,又名 ordered binary tree, sorted binary tree,是一种数据结构。
这种数据结构是用来实现 Abstract Data Type 里面的 Sets(集), Multisets(多重集), Associative Arrays(关联数组)的。
二叉查找树和二叉树的区别在于,所有 node 是经过排序的(方便查找)。
二叉查找树常用于 dynamic sets(动态集)和 lookup tables(查找表)。
node 的定义
通常来说,每个 node 代表的是一条记录(Key-Value Pair),而我们比较的是 node 的 key。
二叉查找树特点
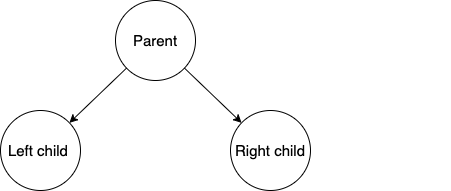
二叉查找树继承了二叉树的优良传统:每个 node 最多只有 2 个 child。
二叉查找树也继承了查找树的特点:parent node key 必须【大于等于】左边的 child node key,并且【小于等于】右边的 child node key。
parent node key ≥ left child key
parent node key ≤ left child key
left child key ≤ right child key
right child key ≥ left child key
node 可以有相同的 key 吗?
根据定义,左右 node 的 key 可以相等,所以二叉查找树里面可以有重复的 key。
5. 一起来创造一颗二叉查找树吧
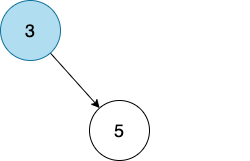
我们先确定一个 root node,比如 3。

然后我们现在要加一个 node,比如 5。
5 大于 3,根据二叉查找树的定义,比 parent node 大的需要放在右边。
我们看一下右边有没有 child。
嗯,没有。
很好,我们现在把 5 放到 3 的右边。
我们再加一个 node,比如 4。
4 > 3,应该放在右边。
可是。。右边已经有 5 了啊,咋办?
那就只好按照先来后到的原则,把 4 作为 5 的 child node 了。
因为 4 < 5,所以我们要把 4 放在 5 的左边。
5 左边有没有 node?
没有!!
太好了,4 找到位置了。
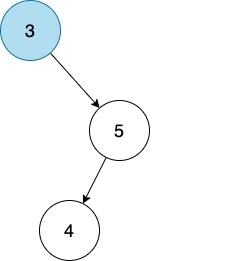
以此类推。
经过不断的比较,我们现在得到了这样一棵树。
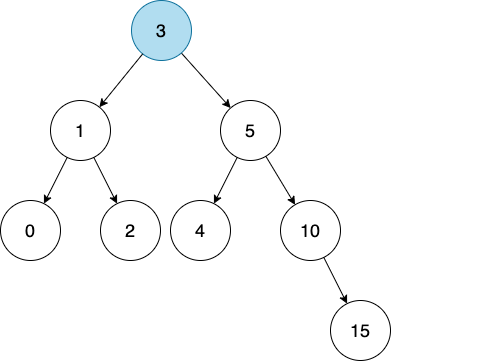
大家请注意看这棵树!
3 作为 root node,它左边所有的数字是不是都比它小?
右边所有的数字是不是都比它大?
每个 node 是不是最多有两个 child?
我们的二叉查找树就完成啦~
6. 插播一节数学课
指数(幂)小知识
幂运算(Exponentiation),表达式为 $b^n$,b 是底数,n 是指数。
比如 2 的 3 次方 = $2^3$ = 2 x 2 x 2 = 8。
对数小知识
对数(Logarithm)是指数的逆运算,用来计算指数。
$b^n$ = x
n = $logb^x$
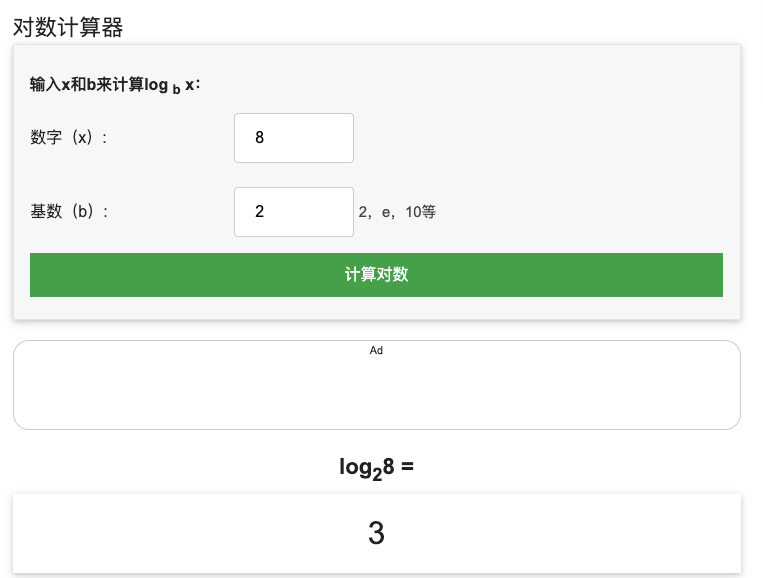
8 以 2 为底的对数 = $log2^8$ = 3
以 2 为底的对数,如 $log2^8$,可以简写为 $log{8}$
7. 二叉查找树与算法
本质上,查找树的设计是基于一个叫做 Binary Search Algorithm 的东西,也就是【二分查找算法】。
比如我们有一颗二叉查找树,树上有从 1 到 100 的 100 个 node,我们想找到 30 这个 node。
因为每个小树枝上的左边的 node 必定小于等于右边 node,所以每个小树枝我们只要查找一次就行了,大大提高了搜索效率。
比如右边 node = 29,左边的所有 node 都必定小于等于 29,就可以省掉很多无用功了。
那我们究竟要找几次呢?
首先,这是一颗二叉树,每个 node 最多两个 child。
我们每次查找可以排除一半的可能性,总共有 100 个 node。
2 的几次方等于 100 呢?
我们可以用刚刚复习过的对数运算来计算 $log2^{100}$,约等于 6.64。
算法里面经常说的时间复杂度,其实就是完成任务所需的时间。
时间越长,任务越复杂。
我们用大写 O 来表示某个算法的时间复杂度。
在二叉查找树里面,寻找某个 node 的时间复杂度就等于 O($log2^{n}$)。
在一颗完全无序的树里面,寻找某个 node 的时间复杂度等于 O($log1^{n}$) = O($n$),这种遍历所有 node 的查找方式被称为 Linear Search(线性查找)。
PS: 这个 $n$ 就是总共的 node 数量(例子里面是 100)。
既然 $log2^{100}$ ≈ 6.64 < $log1^{100}$ = 100,所以二叉查找树的搜索效率就比无序树要快很多啦!!
二叉查找树使得我们可以用高效的 Binary Search 算法来进行搜索,大大节省了计算机所需的时间(懒惰是人类社会的第一生产力)。
8. 结语
本文主要讲了:
- 世上有两种树,一种是二叉树,一种是查找树,其他的树都是它们的孩子……
- 二叉查找树的特点:只有俩孩子,有序,左边小于等于右边。
- 二叉查找树和二分查找算法,解释了为什么二叉查找树的查找效率比无序树要高(基于时间复杂度的比较)。
- 复习了一下对数和指数的基本知识。
听起来很复杂的树结构,是不是其实很简单呢?
希望看完这篇文章,大家都能对【树】有更清晰的认识~
接下来我们还会讨论其他的一些树,敬请期待~
Talk to Luna
Support Luna




