Luna Tech | 聊聊自我平衡树(Self-balancing Tree)

0. 前言
之前我们讲了树结构的基本知识,并且重点讲了二叉查找树。
这一篇我们来看看树结构里面的【自我平衡树】,并且简单介绍一下红黑树。
1. Tree Family
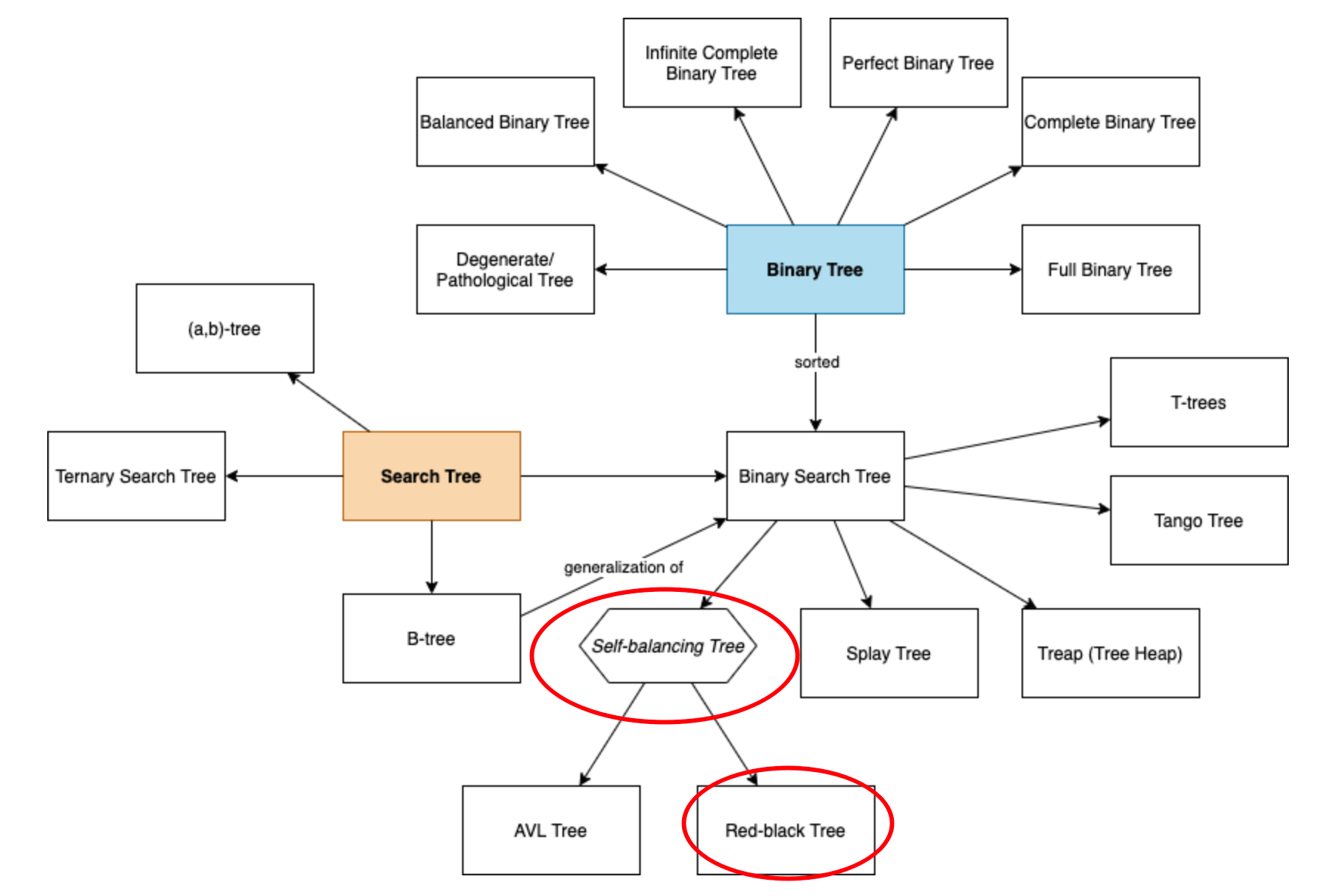
从这张树结构的家族图谱里面,我们可以看到,自我平衡树(Self-Balancing Tree)是一种特殊的二叉查找树。
红黑树是一种自我平衡树。
2. 树的高度(Height)和深度(Depth)
这里先插播一条关于【所有树】的小知识——树的高度和深度。
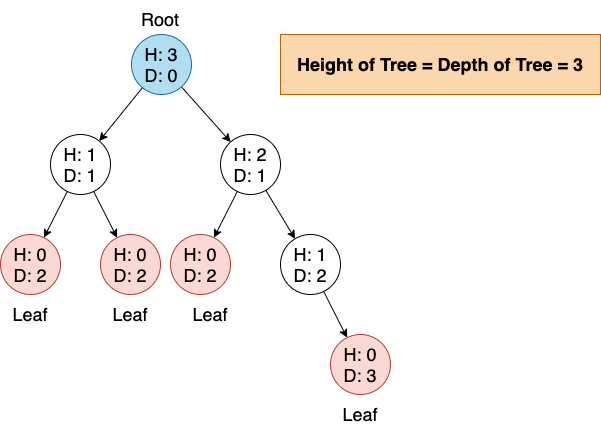
树的高度是从 leaf node 到 root node 的最长距离,而树的深度是从 root node 到 leaf node 的最长距离。
node 的高度是从 leaf node 到这个 node 的最长距离,node 的深度是从 root node 到这个 node 的最长距离。
- 一棵树的高度和深度其实是一样的
- 但每个 node 的高度和深度可能是不同的
- leaf node 的高度是 0,root node 的深度是 0
打个比方,人的高度是从脚(leaf)到头(root);海的深度是从表面(root)到底部(leaf)。
我查资料的时候发现不少人都混淆了这两个概念。。 总体来说,高度用的比较多,但是人们有时候会按照深度的概念来解释高度,😓。
3. Self-balancing Tree(自我平衡树)
从上面的树结构家族图谱里面可以看到,红黑树属于【二叉查找树】中的自我平衡树(Self-balancing Tree)。
那么,自我平衡树是什么意思呢?
二叉查找树的缺点
我们可以回想一下之前讲的二叉查找树,虽然我们认为搜索效率等同于二分查找法,但这个说法其实是不严谨的。
比如下图这种,虽然也是一颗二叉查找树,但是想要找到 4,我们需要从 1 开始找 4 次……
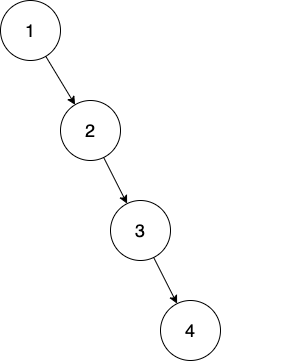
如何解决这样的问题呢?
很简单,如果 n 个 node(节点)可以平均分布在树上,那我们就可以避免这样的悲剧发生了~ 这也就是我们说的【平衡】。
为什么说【自我平衡】?
回到我们一直强调的【增查改删】四种常用数据操作,红黑树的平衡不单单指静态平衡(创建时的平衡),而是一种动态的平衡(增改删照样平衡)。
另外,平衡也不是绝对平衡,而是大致平衡。
平衡保证了二分查找算法 $O(log^n)$ 的时间复杂度,自我平衡保证了树在变化中也能保持大致的动态平衡。
所以我们之前说【二叉查找树】的时间复杂度是 $O(log^n)$ 是不完全正确的。
更确切的说,【自我平衡的二叉查找树】的时间复杂度是 $O(log^n)$ 。
4. Red-Black Tree(红黑树)

红黑树主要用来干嘛?
在 Associative Array 里面,我们提到了两种解决字典问题的方式,1 是 Tree,2 是 Hash Table。
红黑树就是一种 Associative Array 的实现方式。
红黑树的概念
- **两种颜色:**每个 node 都有颜色,要么红,要么黑。
- **根叶为黑:**root node 和所有的 leaf node(‘NIL’ - 无数据)是黑色。
- 每个红色 node 必须有两个黑色 child。
- 从任意一个 node 到 leaf node,必须有相同的黑色 node 数量;
- 红黑树中最长的路径不能超过最短路径的两倍。
- 新的 node 默认是红色。
- 红色 node 不能连续出现。
看到这里你可能有点懵,别怕,我一开始也是满头雾水。 接下来我们会详细解析这些概念。
红黑树的颜色是怎么实现的?
因为红和黑是两种颜色,想要给一个 node 标记颜色,其实只需要增加 1 bit 就够了(01)。
红黑树的高度
在红黑树里面,有个概念叫做**【黑色高度】**(black-height),这个高度指的是从 leaf 到 root 之间的黑色 node 的数量。
因为红黑树概念的第 4 条是:从任意一个 node 到 leaf node,必须有相同的黑色 node 数量。
也就是说,从 root 到 NIL 的黑色 node 数量是相同的。
其他树的高度是从 root 到 leaf 的最长距离,而红黑树的黑色高度则是完全相等的(每条 path 都一样),这也体现了平衡的概念。
注意!!!这里的高度仅仅是黑色高度,不计算红色节点的数量。第五条定义指明,最长路径不能超过最短路径的两倍。
所以下面这个也是一颗合格的红黑树。
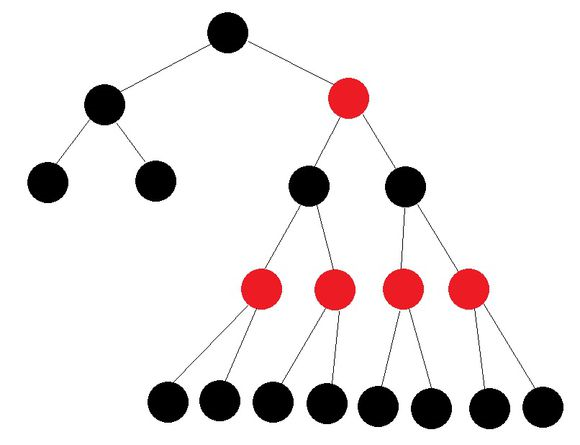
The black height of a red–black tree is the number of black nodes in any path from the root to the leaves, which is constant.
Leaf Node(叶子节点)
红黑树里面的 Leaf node 其实是一个占位符(Placeholder),因为这个 node 只有一个 pointer,里面是不包含任何数据的。
Sentinel Node(哨兵节点)
不包含数据的 Leaf node 用来干嘛呢?
它的本质是一个 Sentinel node(哨兵节点),这种节点可以用在 Linked List 和 Tree 里面,标记遍历路径的终点(Traversal Path Terminator)。
就比如你跑 50 米的时候,起点和终点都有一根线,这样你才知道自己从哪里跑,到哪里就跑完了。
想象一下红黑树的查找,起点是 root node(根节点),终点就是这个 sentinel node。
请思考下面这个问题:
既然红黑树的黑色高度是每条 path 都一样的,我们有必要给每条 path 都标记一个 sentinel node 吗?
答案是:No!
虽然红黑树的图片上看起来有很多的 NIL,但是在实际的应用中,整颗红黑树只需要一个 setinel node(感觉又省了不少 bit)。
5. 结语
本文主要讲了:
- 在二叉查找树的 worst case(最坏情况)下,查找的时间复杂度为 $O(n)$,而不是我们所希望的 $O(log^n)$
- 为了避免这样的悲剧发生,人们设计了一种自我平衡树,自我平衡树是一种特殊的二叉查找树
- 红黑树是一种自我平衡树,它所追求的是【黑色高度】相等,所以严格来讲它不是一颗绝对平衡的树
- 红黑树用了一个额外的 bit 来表示颜色,并且通过一系列的定义和规则,让红色和黑色合理地分配在不同的节点上,从而实现自我平衡(下一篇具体讲)
- 红黑树的叶子节点是不包含任何数据的,只是一个占位符,用来标识树的终点(也就是哨兵节点)
- 在实际的应用中,每棵树只需要一个哨兵节点
- 树的高度指从 leaf 到 root,树的深度指从 root 到 leaf,有时候人们也会乱用这两个概念……
下一篇我们会详细分析红黑树的【增改删】情况,旋转,变色,以及时间复杂度。
大家拜拜啦~
Talk to Luna
Support Luna




